Updated on April 19, 2020.
When I started Artificial Neural Networks and Deep Learning myself, I always stumbled whenever the term ‘activation function‘ popped up anywhere. Once I understood it, the next thing, how do they actually work? Also, what are the most important activation functions and which ones are the best? All these questions are going to be answered here. So, sit tight and read on about activation functions in neural networks.
What are Activation Functions?
Before you read any further go and try to search on the internet the definition of an activation function in regards to neural networks. You will get numerous answers all of which tell the same thing but in a different manner. But that slight change in each answer will make you feel as if each is a different definition.
So, what is an activation function? The first thing to keep in mind, it is actually a function, or rather a mathematical formula. Okay, what does it do? It determines whether a neuron will be fired or not. When all the neurons in a hidden layer of a neural network fire, then the weighted sum of the inputs in addition with the bias becomes the output of that layer. Then this output becomes the input of the next layer. The following figure will help clear up some things:
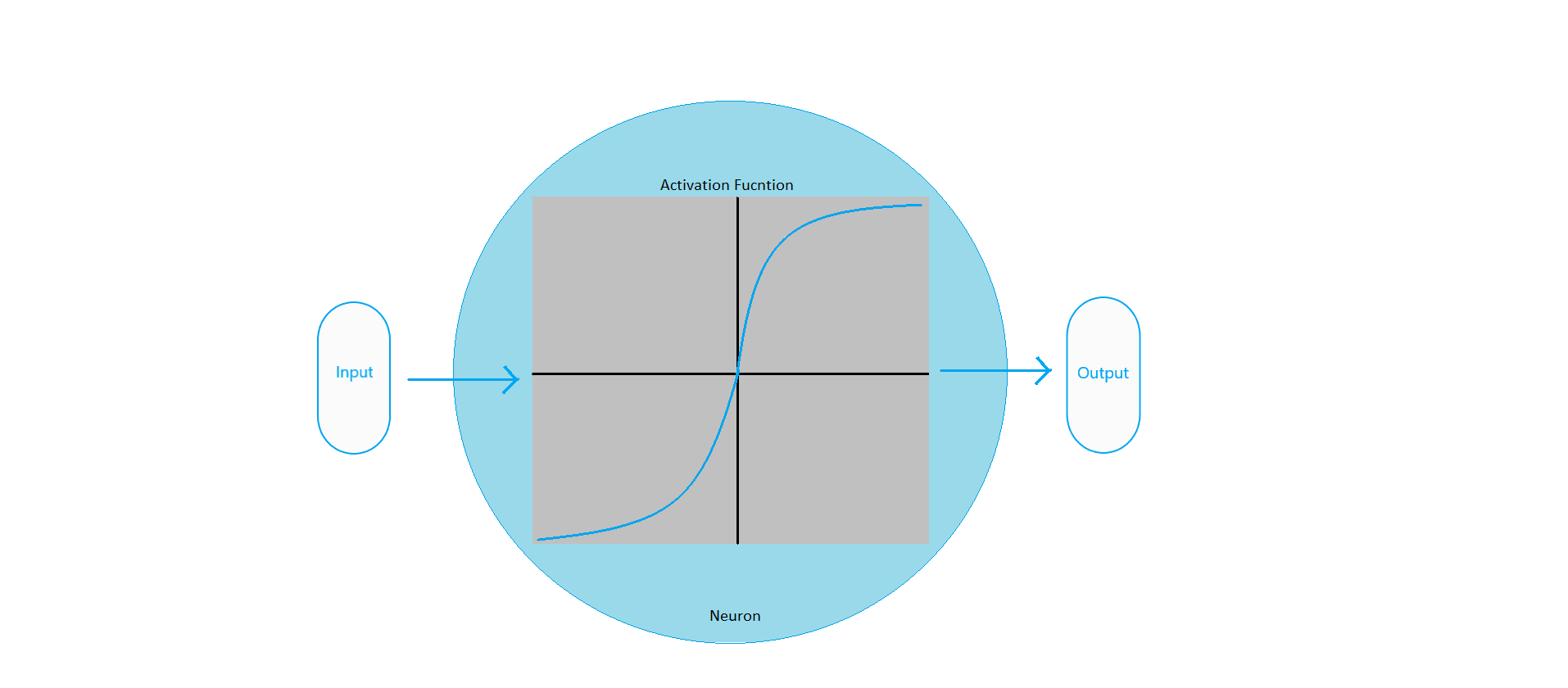
The only thing to keep in mind, you can use the same activation functions for a single neural network. But you can get better results by using different activation functions for the hidden layers and the output layer. More on this part later in the article.
Now, let’s get to know about the different types of activation functions in neural networks.
Linear Activation Function
A Linear Activation Function produces an output which is proportional to the input. The output is the weighted sum of the inputs. This is of the form f(x) = x. If you plot the graph of a linear activation function you will get something similar to the following:
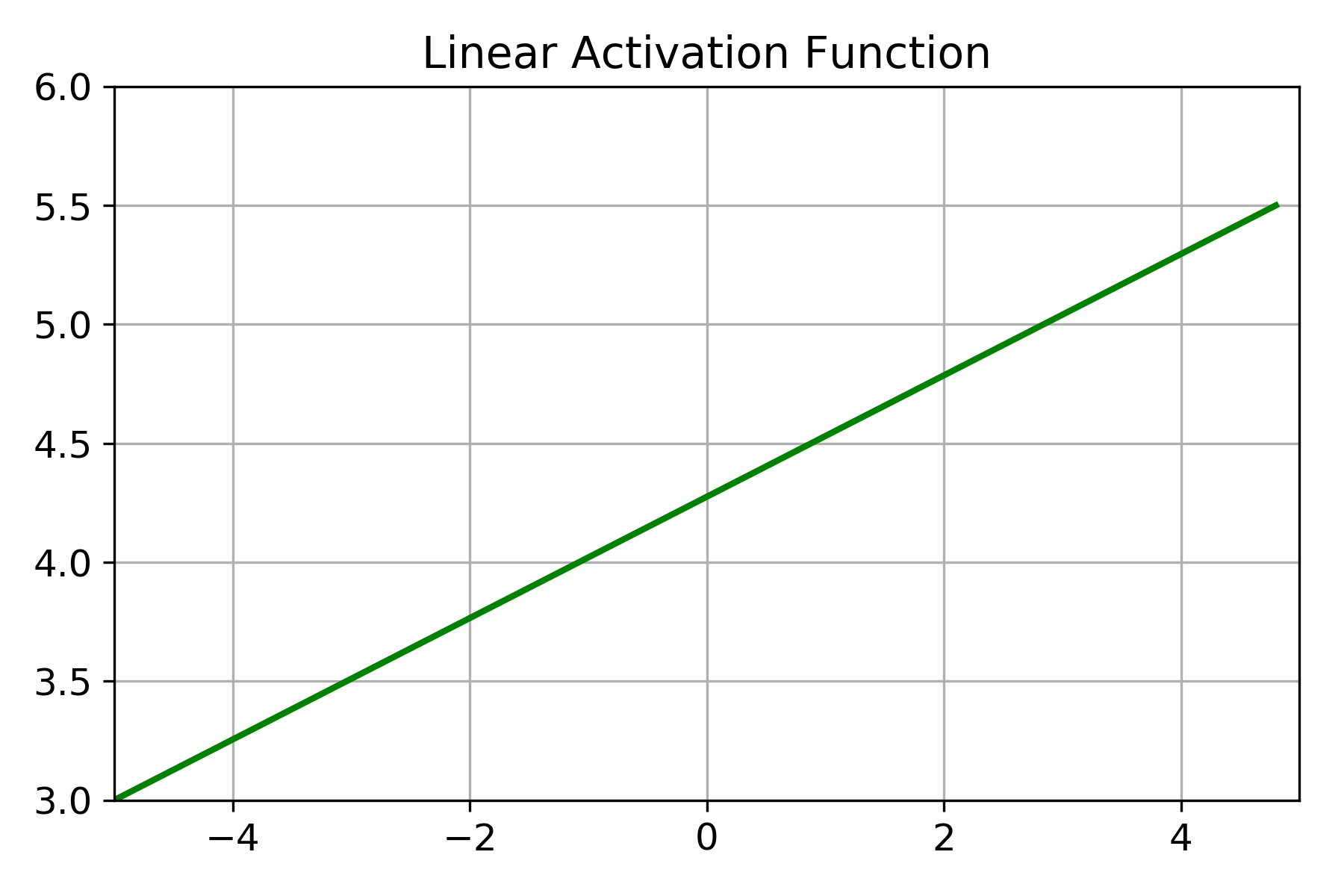
Such functions are also called Identity Functions. But such functions are not very useful in training neural networks. There is a very strong reason behind this. When you use a linear activation function, then a deep neural network even with hundreds of layers will behave just like a single-layer neural network. This is known as a single-layer perceptron. The important takeaway here is that the composition of linear functions will still give a linear function.
So, does that mean linear activation functions are totally useless? Apparently not. They are used and will be used for linear regression where you want the output from a continuous yet somewhat linearly changing dataset.
Non-Linear Activation Functions
As you saw above, for training neural networks, we need non-linear activation functions as linear ones do not help the model to generalize. In this section, you will get to know some of the most commonly used and important non-linear activation functions.
Sigmoid or Logistic Activation Function
The Sigmoid activation function is S – shaped curve. It is a special case of the logistic function. The values scale between 0 and 1 and it is best suited when predicting the probability and also for classification. The function has the following equation:
$$
f(x) = \frac{1}{1 + e^{-x}}
$$
Things will even more clear after you see the following plot of a sigmoidal function:
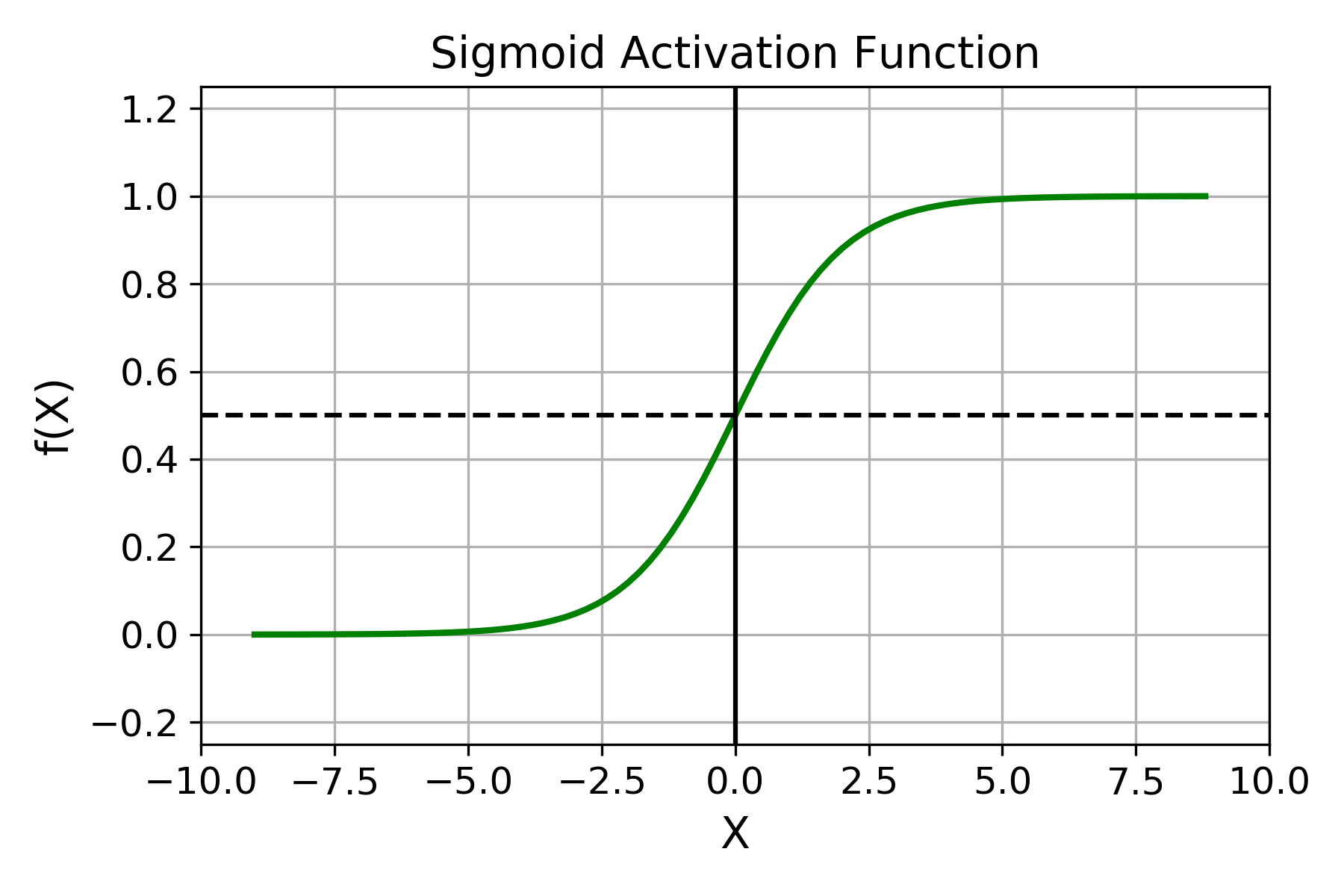
Sigmoid Activation Function
The Sigmoid function is differentiable. Also, unlike the step function or binary step function, the sigmoid activation function gives the indication whether on each step the network is actually moving towards the output or not. It is very suitable for backpropagation.
But nowadays this activation function has lost its utility in most cases. This is because it suffers from vanishing gradient problem. The main overview of this problem is that, for very high and very low values of X, f(X) does not change. This means that the model is difficult to train at those points and the function would not work too effectively.
Hyperbolic Tangent Activation Function (tanh)
The
$$
tanh(x) = 2\sigma(2x) – 1
$$
You can observe the following plot to compare both sigmoid and tanh activation function:
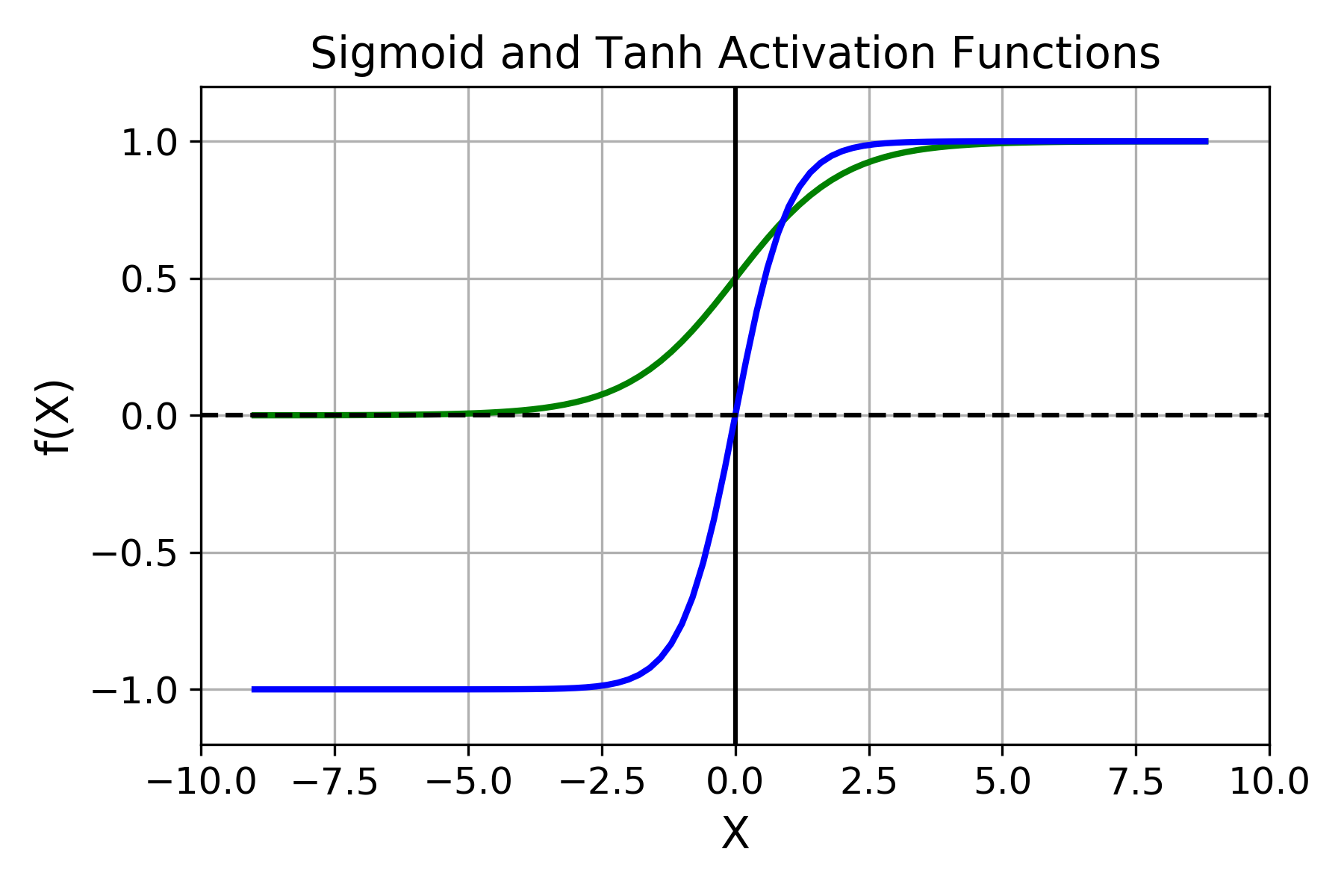
One of the better features of
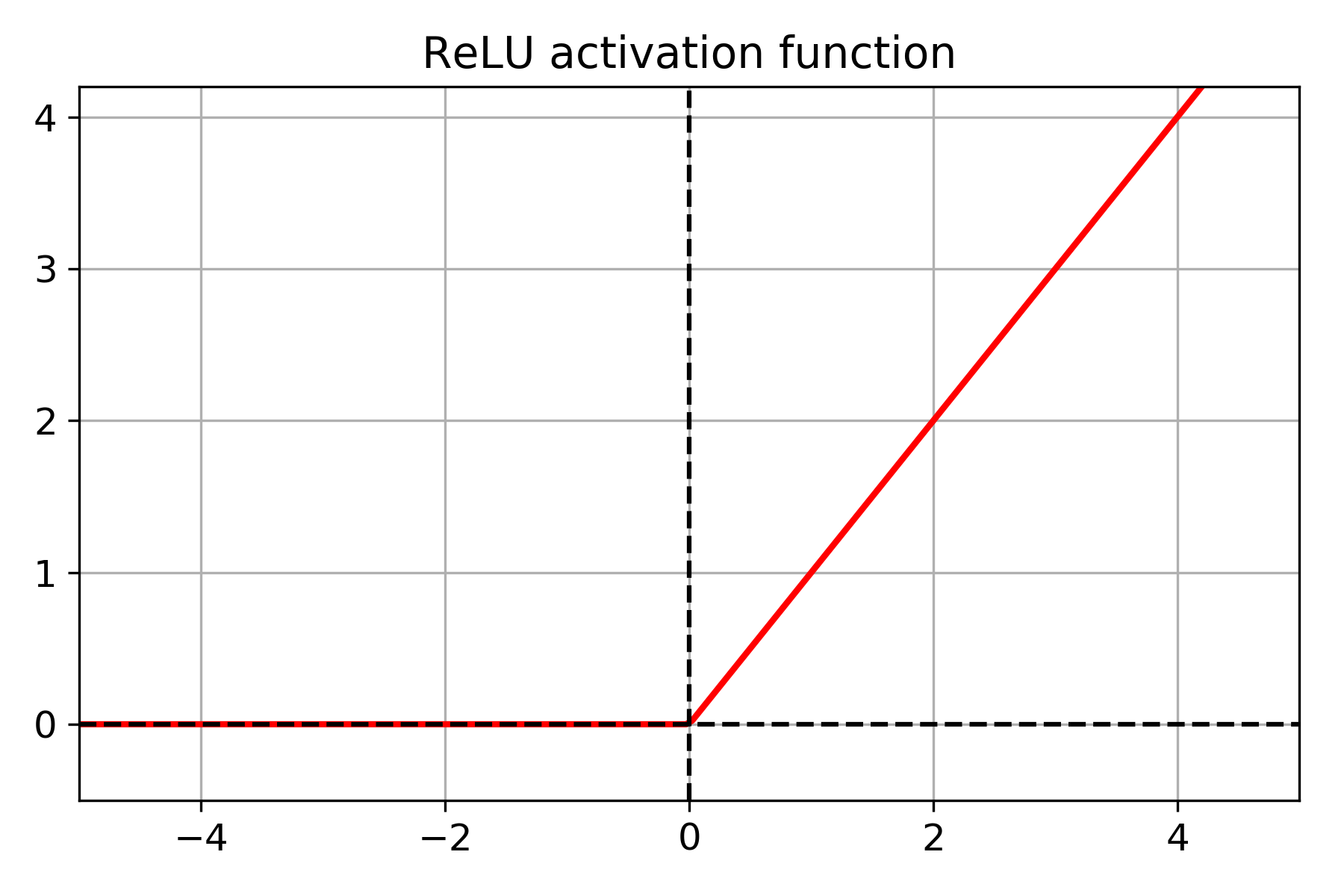
ReLU Activation Function
Rectified Linear Unit or commonly know as ReLU (ReLU(z) = max(0, z)) is perhaps one of the best known practical activation functions.
One of the main reasons for putting so much effort into Artificial Neural Networks (ANNs) is to replicate the functionality of the human brain (the real neural networks). And the human brain mostly seems to function on the basis of sigmoid function. That was the main reason why the sigmoid/ logistic activation function was so popular before.
Now, it
Softmax Activation Function
As you must have noticed from the above discussions, ANNs are mostly used for classification, be it numerical (0 and 1) or labels (disease and no-disease). The activation functions also support that. But for the output layer the Softmax function is a good choice. By using the softmax activation function, the output layer is modified by replacing the individual functions. The outputs will correspond to the calculated probability of the class.
The Right Choice
Generally, for hidden layers, the ReLU activation function should work better than others. It is faster to compute when compared with the logistic and hyperbolic functions. Also, ReLU does not pose any problem when the input values are large. There is no saturation which is clearly visible from the graph.
And for the output layer, if it is a classification task, then the softmax activation function works really well.
EndNote
If you liked this article then comment, share and give a thumbs up. If you have any questions or suggestions, just Contact me here. Be sure to subscribe to the website for more content. Follow me on Twitter, LinkedIn, and Facebook to get regular updates.



The article was quite helpful. Good work!
Thanks. Glad to help. Keep looking out for future posts.