Neural Networks: The Problem of Vanishing Gradients

In neural networks, the backpropagation algorithm is important to train the network. But it also raises another problem. That is the problem of vanishing gradients. In this article, we are going to dive into the topic of vanishing gradients in neural networks and why it is a problem while training.

A Bit About Backpropagation

The backpropagation algorithm is used to update the weights in the network with a Gradient Descent step.

The algorithm goes from the output layer to the lower layers and keeps on propagating the error gradient on the way. So, we can say that the backpropagation algorithm is used to update the parameters in the neural network by calculating the gradient of the cost function.

It starts from the top most layer (the output layer), and keeps on travelling down to the lower layers. Then it computes the gradient of the cost function in relation to all the parameters in the lower layers of the network. At last, these gradients are used to update the parameters in the network.

The Problem: Vanishing Gradients

The above theory looks very useful. But there is a problem. As discussed above, the backpropagation algorithm propagates the error gradient on the way from the top layer (the output layer) to the lower layers until it reaches the input layer.

The gradients keep getting smaller and smaller when moving from the top layer to the lower layers. Due to this, sometimes the weights in the lower layers do not get updated. For that reason, the training of the network is not very effective. Ans this is known as the vanishing gradients problem.

It is not very uncommon for deep neural networks to suffer from the vanishing gradients problems. One of the reasons for this is the use of the logistic sigmoid activation function.

You can read more about the above in this paper by Xavier Glorot and Yoshua Bengio. ( Understanding the difficulty of training deep feedforward neural networks )

You can read one of my previous articles to know more about activation functions.

Let’s look at the plot of the function for better analysis.

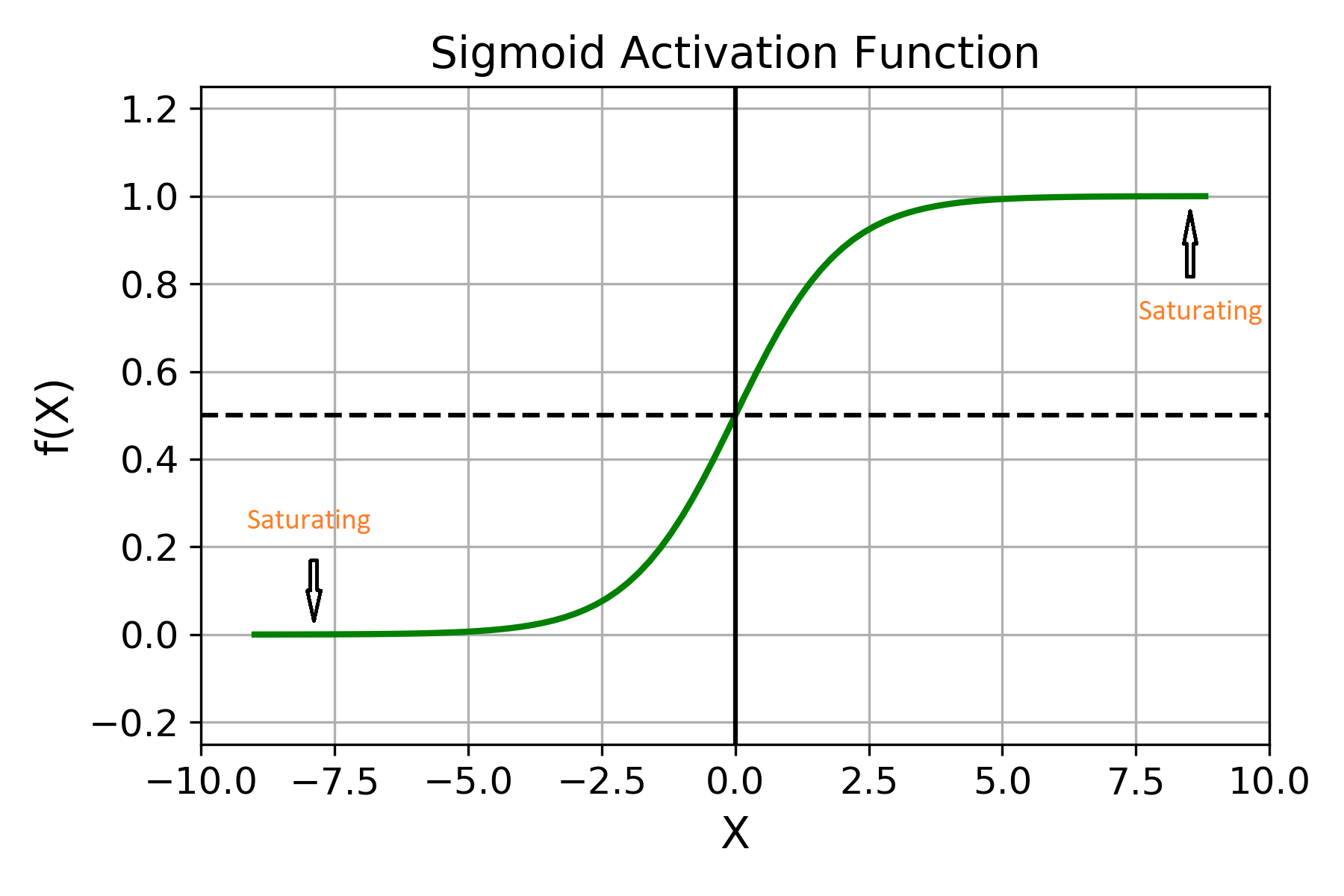
You can see that the logistic sigmoid function ranges from 0 to 1. When the inputs start to become fairly large (positive or negative), the curve starts to saturate towards either 0 or 1. This makes the derivative of the function almost 0. With such low gradients, it becomes almost impossible for the lower layer weights to update.

Moreover, the sigmoid function ranges from 0 to 1, so it has a mean of 0.5 instead of 0. But in training neural networks it is always preferable to have a mean of 0 and a standard deviation of 1.

Solutions and Further Reading

One of the solutions to the above problem is using the hyperbolic tangent activation function having a mean of 0 (as it ranges from -1 to 1). But even this does not solve the problem completely.

Some of the better solutions are the He Initialization and Xavier Initialization. You should surely give these papers a read if you want to know the mathematical details.

Conclusion

This article should act as a primer to increase your knowledge about the problem in backpropagation algorithm and the vanishing gradients problem. You should also try to give the listed papers a brief overview if you do not want to go into much details. If you gained some knowledge through this article, then like, share and subscribe to the newsletter. You can follow me on Twitter and Facebook to get regular updates. You can view my LinkedIn profile here as well.

Liked it? Take a second to support Sovit Ranjan Rath on Patreon!